Les arbres binaires

Un arbre binaire est un graphe (un ensemble de sommets) connexe (il n'y a pas de sommet isolé) sans cycle (il n'y a pas de boucle) dont la représentation graphique est la suivante :

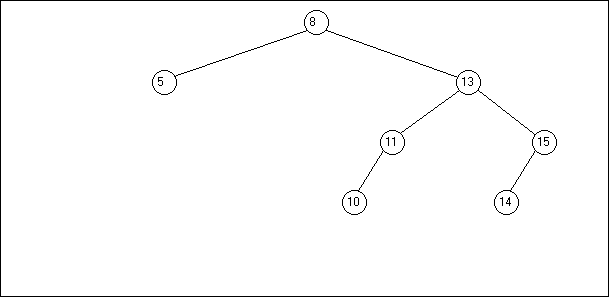L'arbre est dit binaire car chaque noeud possède au plus deux fils : un fils gauche et un fils droit.

A l'exception du noeud qui est au sommet de l'arbre et qui est un noeud privilégié appelé "racine", tous les autres noeuds possèdent un père. Un noeud qui n'a pas de fils est appelé une feuille.

Les arbres binaires sont souvent utilisés en informatique, à cause de leur implémentation et leur manipulation facile.

Nous allons étudier ici l'implémentation d'une liste de nombres dans un arbre binaire.

Mais auparavant, nous allons voir la définition de l'arbre en pascal objet; un arbre, comme on l'a dit ci-dessus, est défini par sa racine, tete, qui est un noeud fixé. Comme on doit parfois se déplacer dans l'arbre sans utiliser obligatoirement une procédure récursive (en raison de sa structure qui s'y prête fortement), on a aussi une variable auxiliaire (nommée courant, de type noeud).

Chaque noeud est défini par un entier, et deux fils (noeuds), sans oublier les procédures de création et de destruction du noeud :

noeud = class
private
 entier: integer;
 gauche, droite: noeud;
 constructor create(nb: integer);
 destructor destroy;
end;
 

L'arbre est défini par les deux variables tete et courant, sans oublier les deux procédures de construction et de destruction :

arbre = class
private
  tete, courant: noeud;
public
 constructor create(nb: integer);
 destructor destroy;
end;

Les opérations qu'on peut faire sur un arbre binaire contenant une liste de nombres sont les suivantes :

1) le parcours et l'affichage

2) l'ajout d'un noeud dans l'arbre

3) le compte du nombre de noeuds d'un arbre

4) le compte du nombre de niveaux

5) l'équilibrage d'un arbre

6) la comparaison de deux arbres

1) Affichage d'un arbre

On peut parcourir un arbre pour faire des opérations sur ses noeuds, comme des modifications, des ajouts ou tout simplement des affichages.

Plusieurs parcours sont possibles pour afficher un arbre :

- les parcours en profondeur

- les parcours en largeur

Les parcours en profondeur

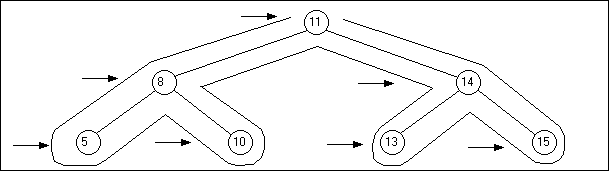
1) Le parcours (ou ordre) préfixé : on affiche le contenu du noeud dès qu'on est dessus, ensuite on parcourt son fils gauche puis son fils droit; le sens du parcours étant indiqué par des flèches liées au trajet (voir le parcours postfixé) :

La procédure permettant de faire un parcours préfixé est la suivante :

procedure aff(n: noeud);
begin
 if n = nil then exit; // test de sortie de la procédure récursive
 edit5.text := edit5.text + intToStr(n.entier) + ';'; // chaîne qui sera affichée
 aff(n.gauche); // parcours fils gauche
 aff(n.droite); // parcours fils droit
end;
 

Ainsi, un parcours préfixé pour cet arbre va nous donner comme résultat :

11;8;5;10;14;13;15

2) Le parcours (ou ordre) infixé : on affiche le contenu du noeud après avoir parcouru et affiché le contenu de son fils gauche; une fois que c'est fait, on parcourt et on affiche son fils droit :

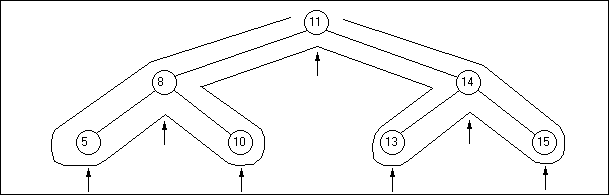La procédure permettant de faire un parcours infixé est la suivante :

procedure aff(n: noeud);
begin
 if n = nil then exit; // test de sortie
 aff(n.gauche); // parcours fils gauche
 edit6.text := edit6.text + intToStr(n.entier) + ';'; // affichage noeud courant
 aff(n.droite); // parcours fils droit
end;
 

On l'appelle avec l'instruction suivante : aff(arbre_nb.tete);

Un parcours infixé pour cet arbre va nous donner comme résultat :

5;8;10;11;13;14;15

On constate que c'est aussi un tri par ordre croissant

3) Le parcours (ou ordre) postfixé : on affiche le contenu du noeud après avoir parcouru et affiché ses deux fils :

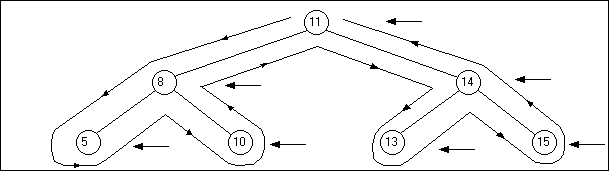La procédure permettant de faire un parcours postfixé est la suivante :

procedure aff(n: noeud);
begin
 if n = nil then exit;
 aff(n.gauche);
 aff(n.droite);
 edit7.text := edit7.text + intToStr(n.entier) + ';';
end;
 

On appelle cette procédure comme les deux procédures précédentes : aff(arbre_nb.tete);

Le parcours en largeur

Le parcours en largeur est défini par le dessin suivant :

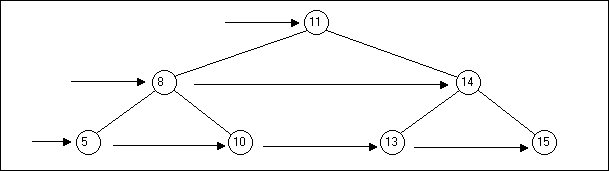Le parcours en largeur n'est pas souvent utilisé dans la manipulation des arbres. Néanmoins, nous allons expliquer la manière dont on le réalise. Le temps requis pour faire ce parcours n'est plus linéaire. Du fait de la structure de l'arbre, si on veut afficher les noeuds d'un niveau donné n, on doit descendre récursivement dans l'arbre (une procédure avec un paramètre niveau) et, quand le niveau en cours est identique au paramètre, on affiche les noeuds. On quitte ensuite la procédure. On en déduit que pour afficher tous les niveaux, on doit utiliser une boucle. Voici la procédure correspondante :

procedure TForm1.Button13Click(Sender: TObject);
var i, j: integer;
 procedure aff(n: noeud; niveau_courant, niveau: integer);
 begin
 if n = nil then exit;
 if niveau = niveau_courant then
 edit9.text := edit9.text + intToStr(n.entier) + ';'
 else
 begin
 aff(n.gauche, niveau_courant + 1, niveau);
 aff(n.droite, niveau_courant + 1, niveau);
 end;
 end;
begin // affichage largeur
 edit9.text := '';
 if arbre_nb = nil then exit;
 j := arbre_nb.compter_niveaux(arbre_nb.tete);
 for i := 1 to j do
 aff(arbre_nb.tete, 1, i);
end;
 

2) Ajout d'un noeud dans un arbre

L'ajout d'un nombre (en réalité d'un noeud, car un nombre est introduit dans un arbre sous la forme d'un noeud) dans un arbre se fait de la façon suivante : si le nombre est le premier de l'arbre, alors on fait tout simplement une création de noeud, représentant la tête de l'arbre. Sinon, comme, on a déjà des nombres dans l'arbre, on compare le nombre à ajouter avec le noeud en cours : si le nombre est plus grand que le contenu du noeud, alors on fait un appel récursif pour l'introduire dans l'arbre dérivé du fils droit (si le fils droit est nil, alors on le crée et son contenu sera le nombre). Mais, si le nombre est plus petit que le contenu du noeud, alors on fait un appel récursif pour l'introduire dans l'arbre dérivé du fils gauche (si le fils gauche est nil, alors on le crée et son contenu sera le nombre qu'on veut introduire).

procedure noeud.ajouter(nb: integer);
begin
 if nb >= entier then
 if droite <> nil then
 droite.ajouter(nb)
 else
 droite := noeud.create(nb)
 else
 if gauche <> nil then
 gauche.ajouter(nb)
 else
 gauche := noeud.create(nb);
end;
 

3) Comptage des noeuds d'un arbre

Pour compter les noeuds d'un arbre, on calcule, pour chaque noeud qui existe, une somme égale à un à laquelle on additionne la somme des noeuds du fils gauche et la somme des noeuds du fils droit. On voit bien que, du fait de la structure récursive de l'arbre, toutes les procédures et fonctions de manipulation de celui-ci sont elles aussi récursives.

function arbre.compter_noeuds(posit: noeud): integer;
begin
 if posit = nil then compter_noeuds := 0
 else
 compter_noeuds := 1 + compter_noeuds(posit.gauche) + compter_noeuds(posit.droite);
end;
 

4) Comptage des niveaux d'un arbre

Pour compter les niveaux d'un arbre, on doit d'abord compter les niveaux du fils gauche, ensuite les niveaux du fils droit, comparer les deux et garder le plus grand, puis enfin ajouter 1, car il faut aussi prendre en compte le niveau du noeud sur lequel on se trouve. En effet, supposons qu'on a un arbre avec seulement la tête. Le fils droit est nil, donc il a 0 niveaux; idem pour le fils gauche. Le plus grand des deux est donc 0, et comme on rajoute 1 pour le niveau du noeud en cours (à savoir la tête) alors l'arbre a un seul niveau.

function arbre.compter_niveaux(posit: noeud): integer;
var ng, nd: integer;
begin
 if posit = nil then compter_niveaux := 0
 else
 begin
 ng := 1 + compter_niveaux(posit.gauche);
 nd := 1 + compter_niveaux(posit.droite);
 if ng > nd then compter_niveaux := ng else compter_niveaux := nd;
 end;
end;
 

5) Equilibrage d'un arbre

Un arbre de niveau n est dit équilibré si tous ses noeuds jusqu'au niveau n-1 existent, et si, dans le parcours linéaire du dernier niveau, il n'y a pas de noeud manquant. C'est ainsi que l'arbre du dessin a) n'est pas équilibré, alors que celui du b) l'est :

a)

b)

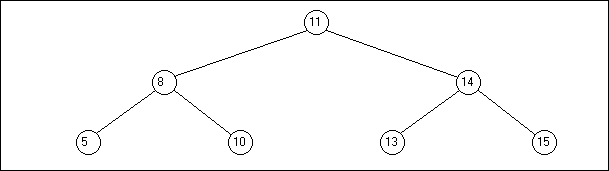Même si le noeud contenant le nombre 15 n'avait pas existé, l'arbre aurait été équilibré, car il respecte bien la définition : tous les noeuds de niveau 2 existent, et, dans le parcours linéaire du dernier niveau, il n'y a pas de noeud manquant.

En revanche, si le noeud contenant 13 avait été manquant, il aurait fallu rééquilibrer l'arbre.

Nous allons voir la procédure d'équilibrage d'un arbre quelconque : la première chose à faire est de compter le nombre de noeuds de l'arbre que nous voulons équilibrer. Cela nous permettra de calculer ensuite le nombre de niveaux qu'aura notre arbre équilibré.

exemples:

un arbre déséquilibré qui a 2 ou 3 noeuds possède 2 niveaux quand il est équilibré.

un arbre qui a de 4 à 7 noeuds possède 3 niveaux quand il est équilibré

un arbre qui a de 8 à 15 noeuds possède 4 niveaux quand il est équilibré

Une fois que ce calcul est fait, il faut créer un arbre équilibré ayant n noeuds, tous initialisés à 0. Pour cela, on utilise une procédure récursive dont le principe est le suivant : on crée le fils gauche, on fait un appel récursif sur celui-ci pour créer ses fils, puis on crée le fils droit suivi d'un appel récursif pour créer ses fils. Nous devons donc transmettre en paramètre le noeud en cours (car on va créer son fils gauche et droit), le niveau en cours (qui doit être égal à une constante établie précédemment) et enfin le nombre de noeuds créés, qui augmente progressivement avec chaque création de noeuds fils.

procedure creer_arbre(n: noeud; niv: integer; var nb_n: integer);
begin
 if nb_n = nb_noeuds then exit; // tous les noeuds nécessaires ont été créés
 if niv < nb_niv then
 begin
 n.gauche := noeud.create(0);
 inc(nb_n);
 creer_arbre(n.gauche, niv + 1, nb_n);
 n.droite := noeud.create(0);
 inc(nb_n);
 creer_arbre(n.droite, niv + 1, nb_n);
 end;
end;
 

Maintenant que cet arbre est créé, il faut le remplir avec les valeurs. Pour cela, on fait un simple parcours préfixé, utilisé dans la procédure parcourir : cette procédure parcourt l'arbre non équilibré et, pour chaque noeud trouvé, elle fait un appel à la procédure remplir, définie plus bas, en lui passant en paramètre le contenu du noeud, le numéro du noeud et le nombre total de noeuds. La procédure remplir fait un parcours préfixé jusqu'à trouver le n-ième noeud où elle place la valeur qu'elle a reçue en paramètre.

procedure parcourir(n: noeud; var nb: integer);
begin
 if n = nil then exit;
 parcourir(n.gauche, nb);
 inc(nb); remplir(arbre_eq.tete, n.entier, nb, nb_noeuds);
 parcourir(n.droite, nb);
end;
 
procedure remplir(n: noeud; valeur, posit, nb_n: integer);
var n1: integer;
begin
 if nb_n = 1 then
 n.entier := valeur
 else
 begin
 n1 := 1;
 while nb_n > n1 do n1 := n1 * 2;
 if posit = (n1 div 2) then
 n.entier := valeur
 else
 if posit < (n1 div 2) then
  remplir(n.gauche, valeur, posit, arbre_nb.compter_noeuds(n.gauche))
 else
 remplir(n.droite, valeur, posit - (n1 div 2), arbre_nb.compter_noeuds(n.droite));
 end;
end;

6) Comparaison de deux arbres

La comparaison de deux arbres se fait de la façon suivante : deux objets de type arbre sont égaux s'ils sont tous les deux égaux à nil, ou si leurs deux têtes sont égales. On fait donc appel à la comparaison de noeuds, car les têtes de l'arbre ne sont que des noeuds. Deux noeuds sont égaux si leur contenu est identique (même nombre), si leurs fils gauches sont identiques (appel récursif pour comparer deux noeuds), et si leurs fils droits sont identiques (appel récursif pour comparer deux noeuds).

function noeud.egal_a(noeud2: noeud): boolean;
begin
 if (self = nil) and (noeud2 = nil) then
 egal_a := true
 else
 if ((self <> nil) and (noeud2 = nil)) or
 ((self = nil) and (noeud2 <> nil)) or
 (entier <> noeud2.entier) then
 egal_a := false
 else
 egal_a := gauche.egal_a(noeud2.gauche) and droite.egal_a(noeud2.droite);
end;
 
function arbre.egal_a(arbre2: arbre): boolean;
begin
 if (self = nil) and (arbre2 = nil) then egal_a := true
 else
 if (self = nil) and (arbre2 <> nil) then egal_a := false
 else
 if (self <> nil) and (arbre2 = nil) then egal_a := false
 else
 egal_a := tete.egal_a(arbre2.tete);
end;

Télécharger le code source Delphi